• Texas Holdem Theory
• Texas Hold'em Theory
• Hook Em Texas

Expected Value [EV] Theory

Expected Value (EV) in Poker is a very misunderstood concept. Our intention here is to explain “expected value” as simply as possible and to make you a better poker player by using expected value theory in your decision making process. Without going into a technical definition here is an example of an event that will have a zero expected value over time (EV = 0.00) so as to make this idea clear in your mind. Let’s say I asked you to pick a number between one and twenty and that each time you got it right I would pay you $20. You would expect to be able to correctly guess the number once out of every twenty tries. If I were to charge you $1 for each guess and you guessed at the number millions of times then the expected value under these circumstances would be zero. You would win $20 every twenty tries and since it would cost you $1 each try you would end up winning $20 for each $20 you gambled. If on the other hand I charged you more than a dollar for each guess you would be silly to bet against me (your expected value would be negative) and if I charged you less than a dollar for each guess then you would want to play against me all day long for the rest of your life. To put this idea into gambling terms you know that in Roulette there are 36 numbers and usually a 0 and even a 00 on a table. Clearly your EV would be zero if the casino paid you 37 to one (plus your original bet back) or 38 to one in total but in fact they give you 35 to one on your bet (and your bet back) so your expected value to make money over time is negative. And that is assuming you are betting on only one number for each spin. If you bet on multiple numbers on the same spin of the wheel then your expected value is even worse.

Texas Hold’em has an easily identifiable structure, alternat- ing between chance nodes and betting rounds in four distinct stages. A high-level view of the imperfect information game tree is shown in Figure 1. Hold’em can be reformulated to produce similar but much smaller games. Texas-hold-em poker-theory poker-strategy  Share. Improve this question. Follow edited Jan 17 '16 at 19:09. 4,950 11 11 silver badges 34 34 bronze badges. These guys didn't just wake up and start playing high stakes poker, they listened, they learned, they practised, they studied. Learn from the best, head over.

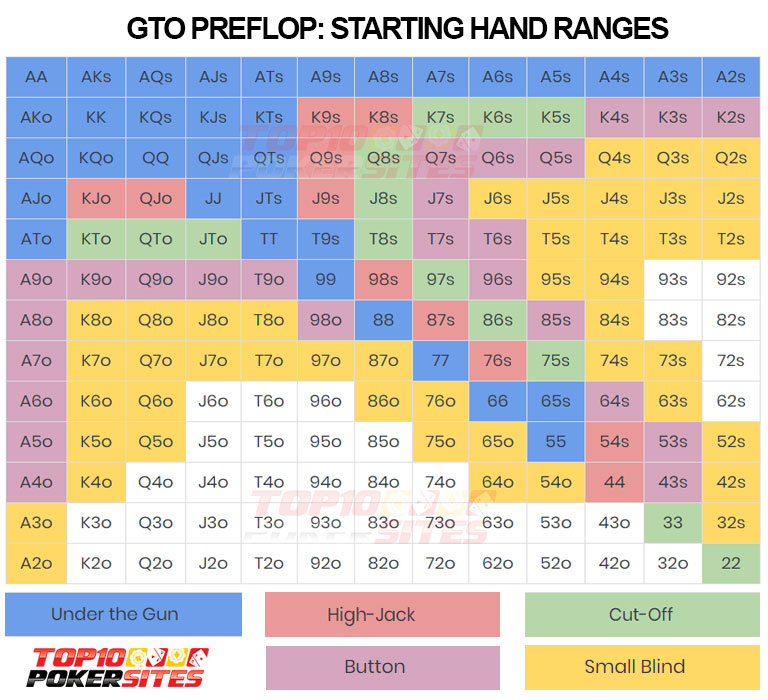
OK now you have a feeling for what we are talking about. How does all this relate to playing Texas Holdem? Glad you asked. In Texas Holdem the expected value of your first two cards depend on the cards you have, your position on the table, and the number of players at the table. In other words you will be happy to know that in the dealer position (on the button) pocket aces yield an EV of 2.96 when there are ten players at the table. This data is based on real data compiled over millions of hands and in real money games. So in the case of our AA in the dealer spot it goes without saying that you will make loads of money with pocket aces. Course we have all lost pocket aces but more often than not we will win the hand and if you have ever played Texas No Limit Holdem then you know that going all in pre-flop with pocket aces is the only time you can be sure to have the one up on all other players in the hand before you have seen a single card. It is expected value theory in Texas Holdem that can help you make a decision to go all in pre-flop (or not). Sometimes you are in a Texas Holdem Tournament and you are running out of chips and it is time to make a bold play (like the all in play). Wouldn’t you rather make a decision that at least you know that in the long run you have a positive expected value with a given hand and not a negative expected value? Sometimes it is just this little difference and this little bit of information that can help you stay in the Tournament until you are in the money as opposed to busting out early. We have taken the liberty to give you all the expected value data for 10 players all the way down to 2 players so that you can make an educated decision in the game at the crucial time instead of gambling blind on any two cards that are yours to play. Ultimately the all in play is the one situation the more talented Texas Hold’em players prefer to avoid in a pre-flop situation (unless they have pocket aces) and by using the all in strategy you will be able to improve your standing in a Texas Holdem Tournament without seeing a flop (hopefully). This is assumed that nobody calls your all in and that you pick up the blinds without a challenge.

As a rule the better the expected value of your first two cards in Texas Holdem the better the chances of you eventually winning the hand. In other words if you have an EV of 1.00 your bet in this situation will get you much more money more often than not as represented by such a strong expected value. You must note that even hands with an EV greater than 1.0 will lose sometimes. But in the long run you will make money with them. Actually the hands with an EV = 0.00 will break even over time so we suggest that you play the two first cards with a positive expected value as often as you can (depending on the situation). If you are in the dealer position with JJ and three people have gone all in for more chips than you have in total and it is your turn to play then you should fold immediately since there is a good probability that someone has a better hand and even though the EV of JJ in the dealer position is 0.89 you have to know that you are up against some very powerful hands.

In the above example we gave you the expected value of JJ in the dealer position in a ten player game. Below you will note the expected value of hands in a ten player game in the dealer position:

If you habitually play hands with large negative expected values you should not be surprised that you are losing more than you win. For example here are some seemingly good and bad starting hands in Texas Holdem and their associated negative expected values (in a ten handed game in the dealer position).

Texas Holdem Theory

Texas Hold'em Theory

To show you the difference position makes in expected value please note below the same hands in the big blind position for a ten handed game:

Hook Em Texas

In other words in the big blind an 8 7 off suit is much worse (you will lose much more money over time playing this hand) than in the dealers position.

Please send all your comments and questions about expected value to info@texasholdemgame.com. Enjoy Online Texas Holdem and play smart!